Generate middle levels Gray codes
Generate all bitstrings of length $2n+1$ with Hamming weight $n$ or $n+1$ by flipping a single bit in each step.| Parameter $n$ (length is $2n+1$) | (max. 15) |
| Algorithm | |
| Initial bitstring | |
| Output format | |
Object info
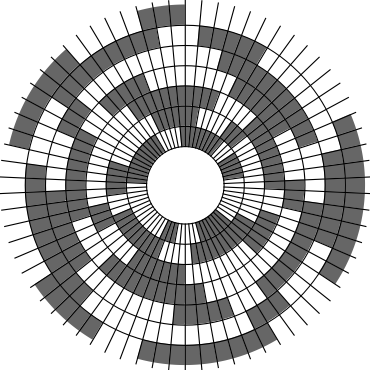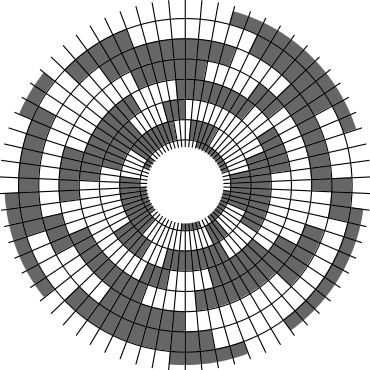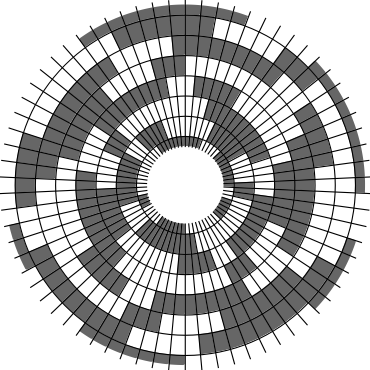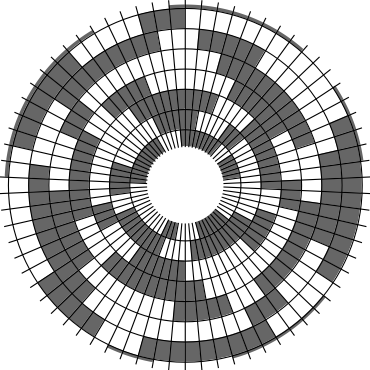
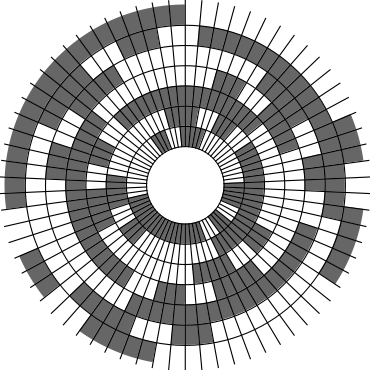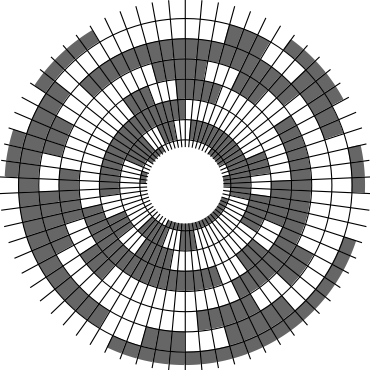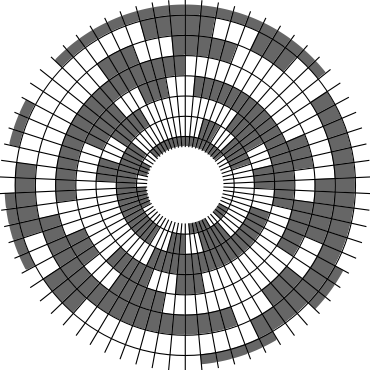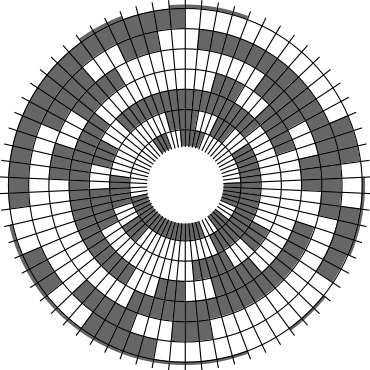
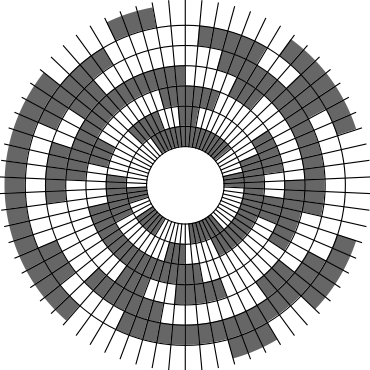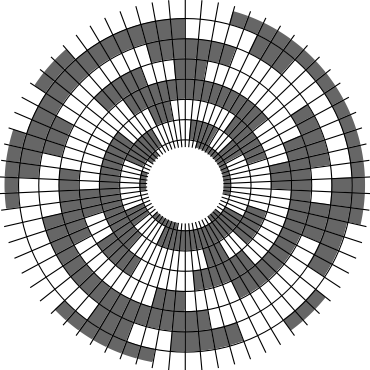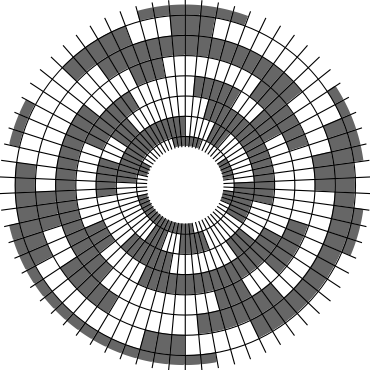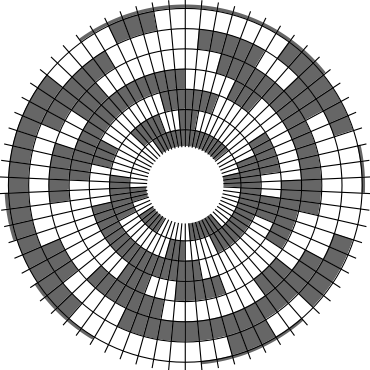
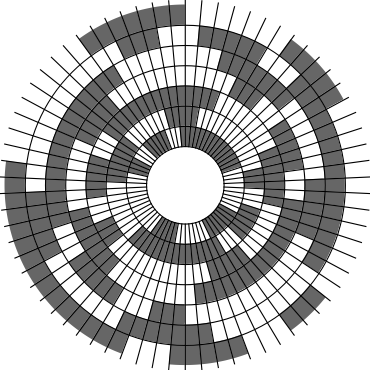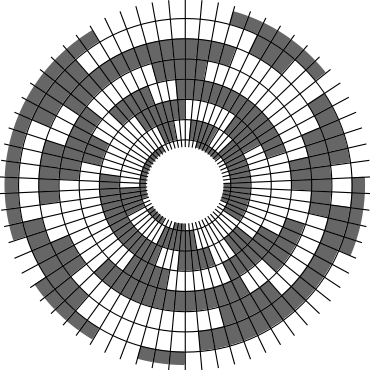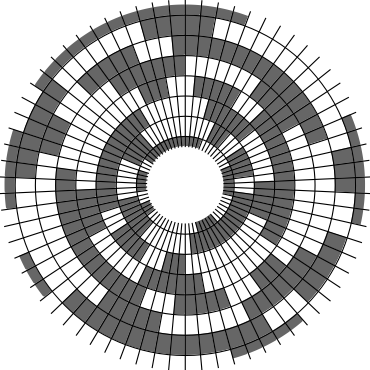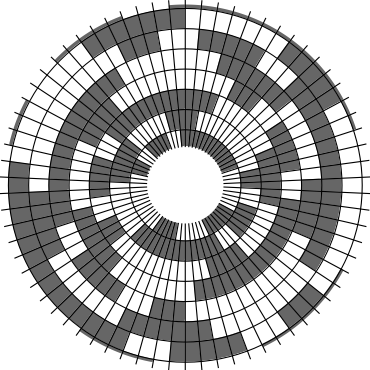
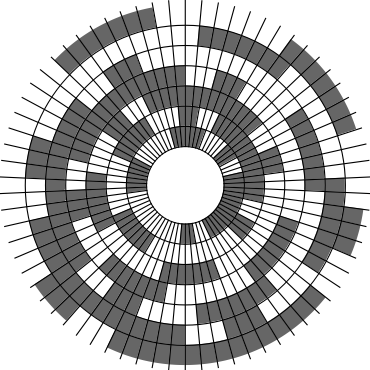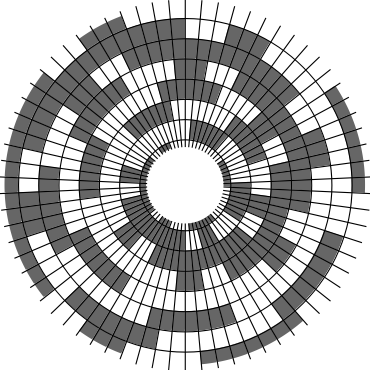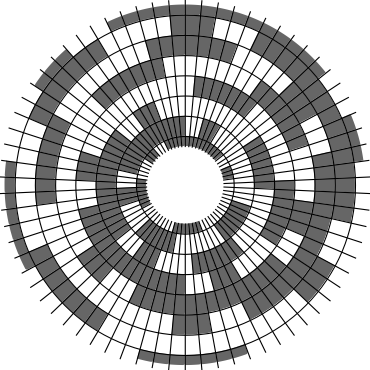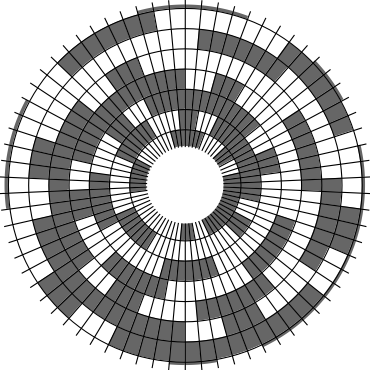
In Problem 56 in Section 7.2.1.3 of his book [Knu11], Knuth raised a stronger version of the middle levels conjecture. He asks for a solution in which the flip sequence, i.e., the sequence of bit positions flipped in each step, can be subdivided into $2n+1$ blocks $\alpha_0,\alpha_1,\ldots,\alpha_{2n}$ of the same length, and the $i$th block $\alpha_i$ is obtained from the initial block $\alpha_0$ by element-wise addition of $i$ modulo $2n+1$ for all $i=1,\ldots,2n$. This allows encoding the entire flip sequence by a factor $2n+1$ more compactly, which was a crucial ingredient in early attempts to tackle the middle levels conjecture experimentally with computer help (see the paper by Shields and Savage [SS99]). For example, such a solution with cyclic symmetry for $n=3$ is given by $\alpha_0=6253462135$. Starting at the bitstring $x=1110000$, applying the flip sequence $\alpha_0$ yields the sequence of strings $1110000,1110010,1010010,1010110,1000110,1001110,\ldots,0111000$, i.e., after 10 flips we reach a bitstring that differs from the initial string $x$ by cyclic right-rotation by one position. More generally, after applying $\alpha_0,\ldots,\alpha_{i-1}$ for all $i=1,\ldots,2n+1$, we reach a copy of $x$ that is cyclically shifted to the right by $i$ positions. Knuth's conjecture was proved by Merino, Mička and Mütze [MMM20] in a more general form, allowing for an arbitrary shift $s\in\{1,\ldots,2n\}$ that is coprime to $2n+1$, i.e., $\alpha_i$ is obtained from $\alpha_0$ by element-wise addition of $i\cdot s$ modulo $2n+1$ for all $i=1,\ldots,2n$. It is not hard to see that the condition on $s$ to be coprime to $2n+1$ is necessary and cannot be omitted. An implementation of this algorithm, using linear time for each generated bitstring, was also provided in the paper [MMM20], and this is the second algorithm running on this website ($(2n+1)$-fold symmetry). The cyclic symmetry can be seen nicely in the wheel diagrams below, which show solutions for $n=3$ and $s=1,\ldots,6$. The animation shifts the bits cyclically around on a torus. Click on each figure to start/stop the animation.
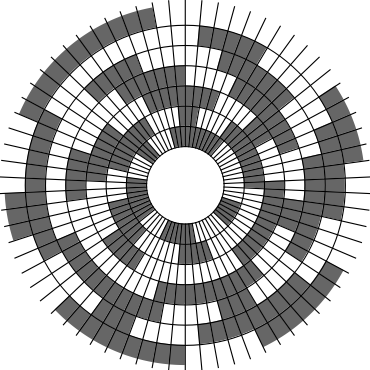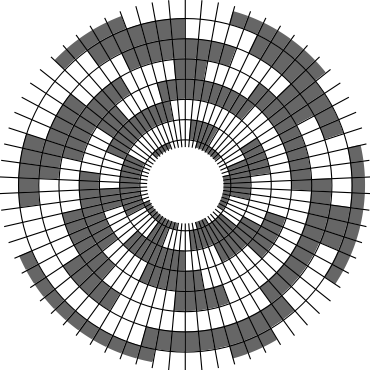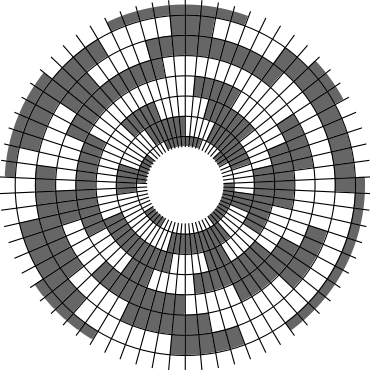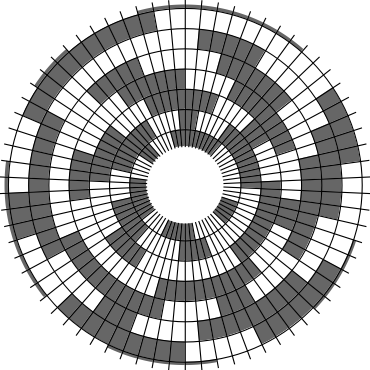
|
|
| $s=1$ | $s=2$ |
| $s=3$ | $s=4$ |
| $s=5$ | $s=6$ |
There are several equivalent formulations of the middle levels conjecture. For instance, the conjecture is equivalent to asking for a listing of all bitstrings of length $2n+2$ with Hamming weight $n+1$ such that any two consecutive bitstrings differ in exchanging the first bit with some other bit (the first bit will alternate between 0 and 1). This is similar to Ehrlich's star transposition Gray code for permutations. The conjecture can also be phrased as follows: Imagine a group of $2n+1$ people, split into two groups of size $n$ and $n+1$ in two rooms that are separated by a revolving door. In each step, one person from the bigger group moves through the door to join the other group. The goal is to come up with a protocol so that each partition into two groups is encountered exactly once.
Enumeration (OEIS)
Download source code
[Zipped C++ source code for the [MMM20] algorithm with $(2n+1)$-fold symmetry (GNU GPL)]
References
- [BW84] M. Buck and D. Wiedemann. Gray codes with restricted density. Discrete Math., 48(2-3):163–171, 1984.
- [GMN18] P. Gregor, T. Mütze, and J. Nummenpalo. A short proof of the middle levels theorem. Discrete Anal., Paper No. 8, 12, 2018.
- [Hav83] I. Havel. Semipaths in directed cubes. In Graphs and other combinatorial topics (Prague, 1982), volume 59 of Teubner-Texte Math., pages 101–108. Teubner, Leipzig, 1983.
- [Knu11] D. E. Knuth. The Art of Computer Programming. Vol. 4A. Combinatorial Algorithms. Part 1. Addison-Wesley, Upper Saddle River, NJ, 2011.
- [MMM20] A. Merino, O. Mička, and T. Mütze. On a combinatorial generation problem of Knuth. In Proceedings of the 2021 ACM-SIAM Symposium on Discrete Algorithms, SODA 2021, pages 735–743, 2021.
- [MN20] T. Mütze and J. Nummenpalo. A constant-time algorithm for middle levels gray codes. Algorithmica, 82(5):1239–1258, 2020.
- [Müt16] T. Mütze. Proof of the middle levels conjecture. Proc. Lond. Math. Soc. (3), 112(4):677–713, 2016.
- [SS99] I. Shields and C. D. Savage. A Hamilton path heuristic with applications to the middle two levels problem. In Proceedings of the Thirtieth Southeastern International Conference on Combinatorics, Graph Theory, and Computing (Boca Raton, FL, 1999), volume 140, pages 161–178, 1999.