Generate colored permutations

A colored permutation of an $n$-element set of objects is a linear ordering of those objects where each element is assigned one of $c$ colors. For example, the colored permutations of $\{1,2,3\}$ where $c=3$ (black, red, blue) are listed below (read top to bottom, left to right):

The above listing can be generated by applying a sequence of prefix reversals, where each color in the reversed prefix is incremented by 1 (modulo $c$). To the right of the permutation listing is the length of the prefix reversal required to go from one permutation to the next.

When $c=2$, we can think of the permutations as a stack of "burnt pancakes" (each pancake is burnt on one side) where a prefix reversal of length $k$ corresponds to flipping the top $k$ pancakes in the stack. For example, the image below illustrates how a stack of 3 pancakes with burnt side up can be sorted so the pancakes are stacked smallest to largest (starting at the top) with burnt side down.

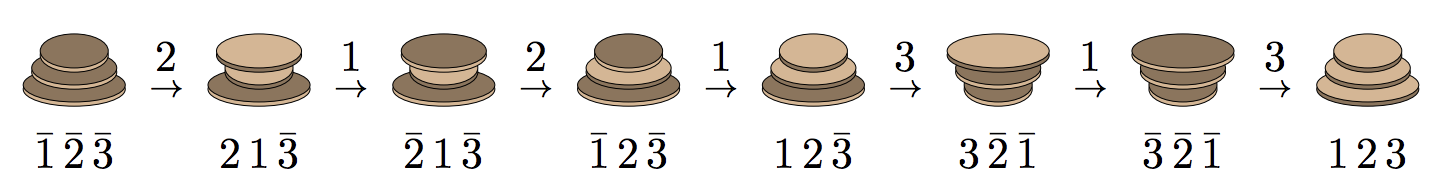
When $c=1$ and $c=2$, both a greedy minimum-flip and maximum-flip strategy will exhaustively list all colored permutations. The same listing can be achieved more efficiently with either recursive or iterative rules by studying the corresponding flip sequence. When $c>2$, the maximum-flip strategy no longer works; however, the minimum-flip strategy will still produce an exhaustive listing of colored permutations with a well-behaved flip sequence (as illustrated above for $n=3$ and $c=3$). The average flip length is constant. The algorithms used above (and available for download below) generate colored permutations in $O(1)$-amortized time per permutation. The listings also enjoy simple and efficient ranking and unranking algorithms which are available in the source code below. Details for the algorithms can be found in [CSW21, SW16a, SW16b, Zak84].

More algorithms for generating one-colored permutations ($c=1$) can be found in the permutations section.

The number of permutations of an $n$-element set with $c$ colors is $c^nn!$.

• $c=1$: OEIS A000142
• $c=2$: OEIS A000165
• $c=3$: OEIS A032031
• $c=4$: OEIS A047053

[C source code (GNU GPL)]

• [CSW21] B. Cameron, J. Sawada, and A. Williams. A Hamilton cycle in the k-sided pancake network. In Combinatorial algorithms, volume 12757 of Lecture Notes in Comput. Sci., pages 137–151. Springer, Cham, 2021.
• [SW16a] J. Sawada and A. Williams. Greedy flipping of pancakes and burnt pancakes. Discrete Appl. Math., 210:61–74, 2016.
• [SW16b] J. Sawada and A. Williams. Successor rules for flipping pancakes and burnt pancakes. Theoret. Comput. Sci., 609(part 1):60–75, 2016.
• [Zak84] S. Zaks. A new algorithm for generation of permutations. BIT, 24(2):196–204, 1984.